Soal dan Pembahasan Gelombang
Soal Dan Jwaban Gelombang
Contoh Soal Gelombang
Soal Soal Gelombang
b. frekuensi sudut gelombang
c. tetapan gelombang
d. cepat rambat gelombang
e. frekuensi gelombang
f. periode gelombang
g. panjang gelombang
h. arah rambat gelombang
i. simpangan gelombang saat t = 1 sekon dan x = 1 m
j. persamaan kecepatan gelombang
k. kecepatan maksimum gelombang
l. persamaan percepatan gelombang
m. nilai mutlak percepatan maksimum
n. sudut fase saat t = 0,1 sekon pada x = 1/3 m
o. fase saat t = 0,1 sekon pada x = 1/3 m
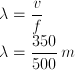
Beda fase gelombang antara dua titik yang jaraknya diketahui adalah


a. menentukan panjang gelombang

b. menentukan frekuensi gelombang

c. menentukan panjang tali

4. Diberikan grafik dari suatu gelombang berjalan seperti gambar di bawah!


atau
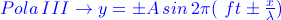
dengan perjanjian tanda sebagai berikut :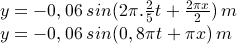
5. Seutas kawat bergetar menurut persamaan :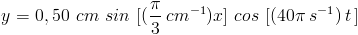
Jarak perut ketiga dari titik x = 0 adalah.....
A. 10 cm
B. 7,5 cm
C. 6,0 cm
D. 5,0 cm
E. 2,5 cm
Sumber Soal : Marthen Kanginan 3A Gejala Gelombang
Pembahasan :
Pola diatas adalah pola untuk persamaan gelombang stasioner ujung tetap atau ujung terikat. Untuk mencari jarak perut atau simpul dari ujung ikatnya, tentukan dulu nilai dari panjang gelombang.
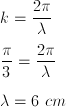
Setelah ketemu panjang gelombang, tinggal masukkan rumus untuk mencari perut ke -3 . Lupa rumusnya,..!?! Atau takut kebalik-balik dengan ujung bebas,..!? Ya sudah tak usah pakai rumus, kita pakai gambar saja seperti di bawah:
Posisi perut ketiga P3 dari ujung tetap A adalah satu seperempat panjang gelombang atau (5/4) λ (Satu gelombang = satu bukit - satu lembah), sehingga nilai X adalah :
X = (5/4) λ = (5/4) x 6 cm = 7,5 cm
Disqusion
1. Question English
→ Sebuah gelombang berjalan dari titik A ke B dengan kelajuan 5 m/s. Periode gelombang tersebut adalah 0,4 s. Jika selisih fase antara titik A dan B adalah 6π/5 maka jarak AB adalah.....
A. 0,6 m
B. 0,8 m
C. 1,0 m
D. 1,2 m
E. 1,4 m
Answer Discusion
The informations that we can get from above problem are:
wave speed ν = 5 m/sec
wave period T = 0.4 sec
AB phase (angle) difference Δθ = 6π/5
or
AB phase difference Δφ = 6π/5 : 2π = 3/5
AB = ....m
Use the wave basic formula to find the wavelength first,
λ = Tν = (0.4 sec)(5 m/sec) = 2 m
as we know that the phase difference between two points (A and B) :
Δφ = x/λ where x is the AB distance. So then
3/5 = x/2
x = (2)(3/5) = 6/5 = 1.2 m
2. Question English
Given a standing wave equation traveling along a string:
y = 0.2 sin (5πx) cos (20πt)
with y and x in m and t in sec. Find the wave speed!
Pertanyaan Indonesia
→Berikut persamaan sebuah gelombang stationer pada tali
y = 0.2 sin (5πx) cos (20πt)
y dan x dalam satuan meter dan t dalam sekon. Tentukan kecepatan gelombang!
Discussion Answer
Use the standing wave equation form:
y = 2A sin kx cos ωt
y = 0.2 sin (5πx) cos (20πt)
Find the values of wavelength (λ) and wave frequency (f) to find the wave speed ( velocity):
k = 5π as we knew in the previous, that k = 2π/λ
so then
5π = 2π/λ
λ = 0.4 m
ω = 20π as we knew ω = 2πf
so then
20π = 2πf
f = 10 Hz
The relationship between λ, f and ν :
ν = λ f
so then we get
ν = (0.4)(10) = 4 m.s−1
Question 3
Given two equations of traveling waves on a string:
y = 0.04 sin (2πx + 10πt)
y = 0.04 sin (2πx − 10πt)
with y and x in m and t in sec. Find magnitude of standing wave amplitude that is formed by these two waves for x = 1/12 m!
Pertanyaan Indonesia
→Berikut dua buah persamaan gelombang berjalan sinusoidal pada sebuah tali:
y = 0.04 sin (2πx + 10πt)
y = 0.04 sin (2πx − 10πt)
dengan y dan x dalam satuan m dan t dalam satuan s. Tentukan besar amplitudo gelombang stationer yang dihasilkan oleh superposisi dua buah gelombang tersebut untuk nilai x = 1/12 m!
Answer Discussion
These two sinusoidal waves have the same wavelength and amplitude and traveling in opposite directions. The first is to the left, the second is to the rigth direction. By applying the superposition principle we'll get a standing wave equation:
y = 2A sin kx cos ω t
so we have to get the needed quantities from the two above:
A = 0.04 m
ω = 10π
k = 2π
so then our equation becomes
y = 2(0.04) sin 2πx cos 10π t
y = 0.08 sin 2πx cos 10π t
0.08 sin 2πx that what we called the amplitude of standing wave (As). For x = 1/4 m
As = 0.08 sin 2πx
As = 0.08 sin 2π(1/12)
As = 0.08 sin (π/6)
As = 0.08 (0.5) = 0.04 m
Question 4
A wave travels through points A and B, in A to B direction. When t = 0 the wave displacement at point A is 0. Known that A and B is 8 cm apart, the wavelength and the amplitude are 12 cm and 4 cm respectively. Determine the wave displacement at point B when the phase of point A is 3π/2!
→Suatu gelombang berjalan melalui titik A dan B yang berjarak 8 cm dalam arah dari A ke B. Pada saat t = 0 simpangan gelombang di A adalah 0. Jika panjang gelombangnya adalah 12 cm dan amplitudonya = 4 cm, tentukan simpangan titik B pada saat fase titik A 3π/2!
Discussion
Traveling wave equation for point B:
YB = A sin 2π ( t/T − x/λ)
2 π t/T = 3π/2
t/T = 3/4
YB = 4 sin 2π ( 3/4 − 8/12)
YB = 4 sin 2π ( 9/12 − 8/12)
YB = 4 sin ( π/6 ) = 4 sin 30° = 4 ( 0.5) = 2 cm
Literatur: fisikastudycenter.com
Soal Dan Jwaban Gelombang
Contoh Soal Gelombang
Soal Soal Gelombang
1. Diberikan sebuah persamaan gelombang Y = 0,02 sin (10πt − 2πx) dengan t dalam sekon, Y dan x dalam meter. Tentukan :
a. amplitudo gelombangb. frekuensi sudut gelombang
c. tetapan gelombang
d. cepat rambat gelombang
e. frekuensi gelombang
f. periode gelombang
g. panjang gelombang
h. arah rambat gelombang
i. simpangan gelombang saat t = 1 sekon dan x = 1 m
j. persamaan kecepatan gelombang
k. kecepatan maksimum gelombang
l. persamaan percepatan gelombang
m. nilai mutlak percepatan maksimum
n. sudut fase saat t = 0,1 sekon pada x = 1/3 m
o. fase saat t = 0,1 sekon pada x = 1/3 m
Pembahasan :
Bentuk persamaan umum gelombang:
Y = A sin (ωt - kx)
dengan A amplitudo gelombang, ω = 2πf dan k=2π/λ dengan demikian :
a. A = 0,02 m
b. ω = 10π rad/s
c. k = 2π
d. v = ω/k = 10π/2π = 5 m/s
c. k = 2π
d. v = ω/k = 10π/2π = 5 m/s
e. f = ω/2π = 10π/2π = 5 Hz
f. T = 1/f = 1/ 5 = 0, 2 sekon
g. λ = 2π/k = 2π/2π = 1 m
h. ke arah sumbu x positif
i. Y = 0,02sin(10 π- 2π)=0,02sin(8π)= 0 m
j. v = ω A cos(ωt−kx)=10π(0,02) cos(10πt−2πx) m/s
k. vmaks = ωA = 10π(0,02) m/s
l. a = −ω2y=−(10π)2 (0,02)sin(10πt−2πx) m/s2
m. amaks =|−ω2A|=|−10π2 (0,02)| m/s2
n. sudut fase θ = (10.π.0,1−2π.(1/3)=1/3 π = 60o
o. fase φ = 60o/360o = 1/6
j. v = ω A cos(ωt−kx)=10π(0,02) cos(10πt−2πx) m/s
k. vmaks = ωA = 10π(0,02) m/s
l. a = −ω2y=−(10π)2 (0,02)sin(10πt−2πx) m/s2
m. amaks =|−ω2A|=|−10π2 (0,02)| m/s2
n. sudut fase θ = (10.π.0,1−2π.(1/3)=1/3 π = 60o
o. fase φ = 60o/360o = 1/6
2. Suatu gelombang permukaan air yang frekuensinya 500 Hz merambat dengan kecepatan 350 m/s. tentukan jarak antara dua titik yang berbeda sudut fase 60°! (Sumber : Soal SPMB)
Pembahasan :
Lebih dahulu tentukan besarnya panjang gelombang dimana
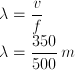
Beda fase gelombang antara dua titik yang jaraknya diketahui adalah

3. Seutas tali salah satu ujungnya digerakkan naik turun sedangkan ujung lainnya terikat. Persamaan gelombang tali adalah y = 8 sin (0,1π) x cos π (100t - 12) dengan y dan x dalam cm dan t dalam satuan sekon. Tentukan:
a. panjang gelombang
b. frekuensi gelombang
c. panjang tali
(Sumber : Soal Ebtanas)
Pembahasan :
Pola dari gelombang stasioner diatas adalah

a. menentukan panjang gelombang

b. menentukan frekuensi gelombang

c. menentukan panjang tali

4. Diberikan grafik dari suatu gelombang berjalan seperti gambar di bawah!
Jika jarak P ke Q ditempuh dalam waktu 5 sekon, tentukan persamaan dari gelombang di atas! (Tipikal Soal UN)
Pembahasan :
Bentuk umum persamaan gelombang adalah

atau

atau
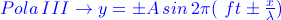
dengan perjanjian tanda sebagai berikut :
Tanda Amplitudo (+) jika gerakan pertama ke arah atas
Tanda Amplitudo (-) jika gerakan pertama ke arah bawah
Tanda dalam kurung (+) jika gelombang merambat ke arah sumbu X negatif / ke kiri
Tanda dalam kurung (-) jika gelombang merambat ke arah sumbu X positif / ke kanan
ambil data dari soal panjang gelombang (λ) = 2 meter, dan periode (T) = 5/2 sekon atau frekuensi (f) = 2/5 Hz, masukkan data ke pola misal pola ke 2 yang dipakai didapat
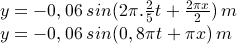
5. Seutas kawat bergetar menurut persamaan :
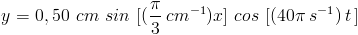
Jarak perut ketiga dari titik x = 0 adalah.....
A. 10 cm
B. 7,5 cm
C. 6,0 cm
D. 5,0 cm
E. 2,5 cm
Sumber Soal : Marthen Kanginan 3A Gejala Gelombang
Pembahasan :
Pola diatas adalah pola untuk persamaan gelombang stasioner ujung tetap atau ujung terikat. Untuk mencari jarak perut atau simpul dari ujung ikatnya, tentukan dulu nilai dari panjang gelombang.
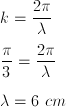
Setelah ketemu panjang gelombang, tinggal masukkan rumus untuk mencari perut ke -3 . Lupa rumusnya,..!?! Atau takut kebalik-balik dengan ujung bebas,..!? Ya sudah tak usah pakai rumus, kita pakai gambar saja seperti di bawah:
Posisi perut ketiga P3 dari ujung tetap A adalah satu seperempat panjang gelombang atau (5/4) λ (Satu gelombang = satu bukit - satu lembah), sehingga nilai X adalah :
X = (5/4) λ = (5/4) x 6 cm = 7,5 cm
Disqusion
1. Question English
A wave travels from point A to point B with a speed of 5 m/sec. The wave period is 0.4 sec and the phase difference between A and B is 6π/5, then the AB distance is....
A. 0.6 m
B. 0.8 m
C. 1.0 m
D. 1.2 m
E. 1.4 m
A. 0.6 m
B. 0.8 m
C. 1.0 m
D. 1.2 m
E. 1.4 m
Diskusi
Pertanyaan Indonesia → Sebuah gelombang berjalan dari titik A ke B dengan kelajuan 5 m/s. Periode gelombang tersebut adalah 0,4 s. Jika selisih fase antara titik A dan B adalah 6π/5 maka jarak AB adalah.....
A. 0,6 m
B. 0,8 m
C. 1,0 m
D. 1,2 m
E. 1,4 m
Answer Discusion
The informations that we can get from above problem are:
wave speed ν = 5 m/sec
wave period T = 0.4 sec
AB phase (angle) difference Δθ = 6π/5
or
AB phase difference Δφ = 6π/5 : 2π = 3/5
AB = ....m
Use the wave basic formula to find the wavelength first,
λ = Tν = (0.4 sec)(5 m/sec) = 2 m
as we know that the phase difference between two points (A and B) :
Δφ = x/λ where x is the AB distance. So then
3/5 = x/2
x = (2)(3/5) = 6/5 = 1.2 m
2. Question English
Given a standing wave equation traveling along a string:
y = 0.2 sin (5πx) cos (20πt)
with y and x in m and t in sec. Find the wave speed!
Pertanyaan Indonesia
→Berikut persamaan sebuah gelombang stationer pada tali
y = 0.2 sin (5πx) cos (20πt)
y dan x dalam satuan meter dan t dalam sekon. Tentukan kecepatan gelombang!
Discussion Answer
Use the standing wave equation form:
y = 2A sin kx cos ωt
y = 0.2 sin (5πx) cos (20πt)
Find the values of wavelength (λ) and wave frequency (f) to find the wave speed ( velocity):
k = 5π as we knew in the previous, that k = 2π/λ
so then
5π = 2π/λ
λ = 0.4 m
ω = 20π as we knew ω = 2πf
so then
20π = 2πf
f = 10 Hz
The relationship between λ, f and ν :
ν = λ f
so then we get
ν = (0.4)(10) = 4 m.s−1
Question 3
Given two equations of traveling waves on a string:
y = 0.04 sin (2πx + 10πt)
y = 0.04 sin (2πx − 10πt)
with y and x in m and t in sec. Find magnitude of standing wave amplitude that is formed by these two waves for x = 1/12 m!
Pertanyaan Indonesia
→Berikut dua buah persamaan gelombang berjalan sinusoidal pada sebuah tali:
y = 0.04 sin (2πx + 10πt)
y = 0.04 sin (2πx − 10πt)
dengan y dan x dalam satuan m dan t dalam satuan s. Tentukan besar amplitudo gelombang stationer yang dihasilkan oleh superposisi dua buah gelombang tersebut untuk nilai x = 1/12 m!
Answer Discussion
These two sinusoidal waves have the same wavelength and amplitude and traveling in opposite directions. The first is to the left, the second is to the rigth direction. By applying the superposition principle we'll get a standing wave equation:
y = 2A sin kx cos ω t
so we have to get the needed quantities from the two above:
A = 0.04 m
ω = 10π
k = 2π
so then our equation becomes
y = 2(0.04) sin 2πx cos 10π t
y = 0.08 sin 2πx cos 10π t
0.08 sin 2πx that what we called the amplitude of standing wave (As). For x = 1/4 m
As = 0.08 sin 2πx
As = 0.08 sin 2π(1/12)
As = 0.08 sin (π/6)
As = 0.08 (0.5) = 0.04 m
Question 4
A wave travels through points A and B, in A to B direction. When t = 0 the wave displacement at point A is 0. Known that A and B is 8 cm apart, the wavelength and the amplitude are 12 cm and 4 cm respectively. Determine the wave displacement at point B when the phase of point A is 3π/2!
→Suatu gelombang berjalan melalui titik A dan B yang berjarak 8 cm dalam arah dari A ke B. Pada saat t = 0 simpangan gelombang di A adalah 0. Jika panjang gelombangnya adalah 12 cm dan amplitudonya = 4 cm, tentukan simpangan titik B pada saat fase titik A 3π/2!
Discussion
Traveling wave equation for point B:
YB = A sin 2π ( t/T − x/λ)
2 π t/T = 3π/2
t/T = 3/4
YB = 4 sin 2π ( 3/4 − 8/12)
YB = 4 sin 2π ( 9/12 − 8/12)
YB = 4 sin ( π/6 ) = 4 sin 30° = 4 ( 0.5) = 2 cm
Literatur: fisikastudycenter.com









